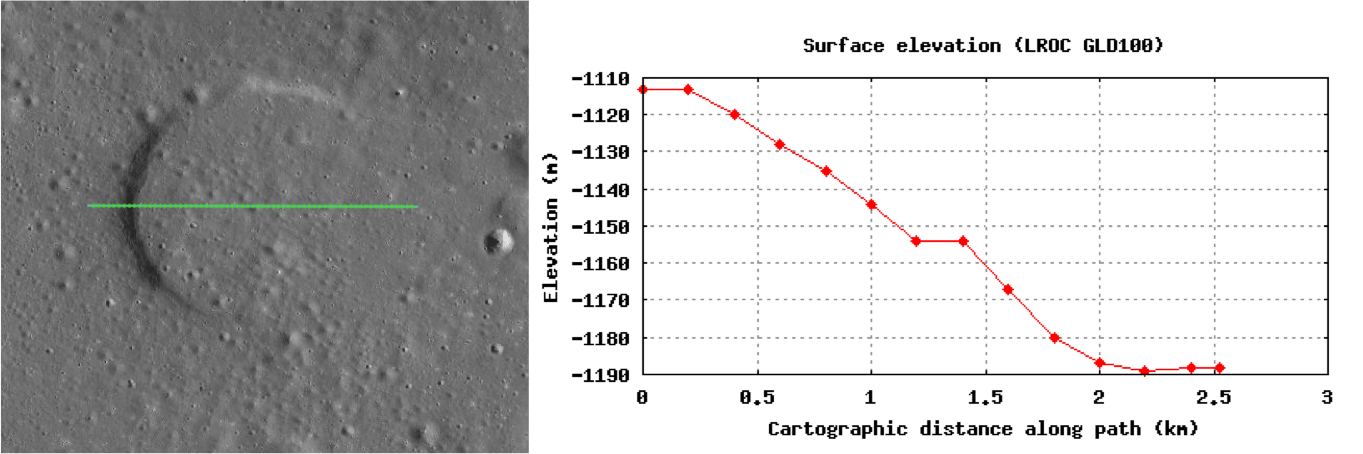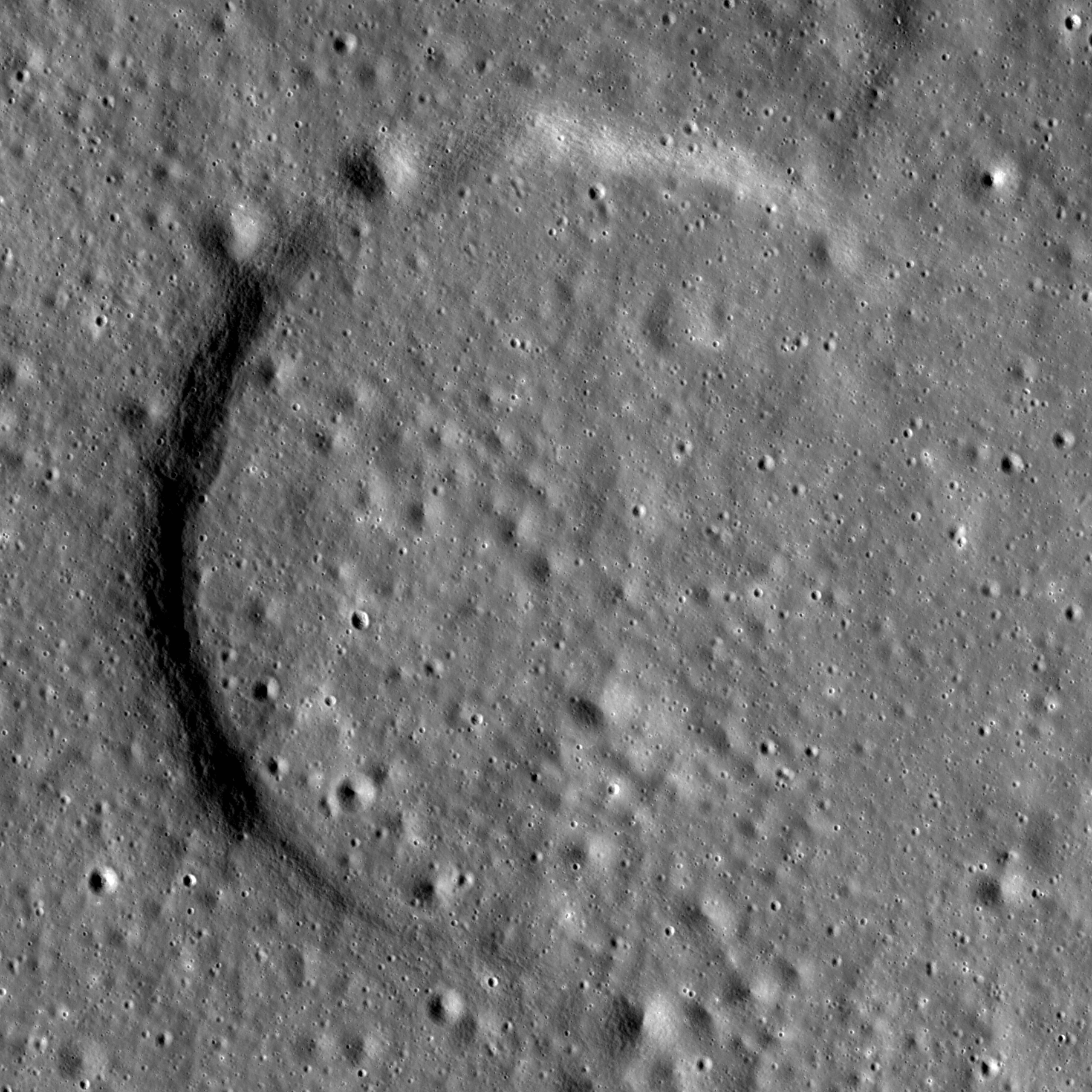
Today’s Featured Image is a remnant of an unnamed crater located in the Rimae Prinz region of Oceanus Procellarum. Since geologists use the term crater to describe any hole in the ground, the term crater is further differentiated by its formation mechanism. Craters on the Moon were formed either by volcanic activity (explosion or collapse) or impacts (asteroids and comets). What clues can be found for this degraded crater that may reveal its formation mechanism? First check for a raised rim; craters formed by an impact have a raised rim because material is excavated and projected outward and the substrate is uplifted, whereas those formed by volcanic activity typically do not have a raised rim. The LROC GLD100 model provides a way to inspect the topography along the crater exterior, rim and interior (the green line in the image below). In this case there is no elevated rim, suggestive of a volcanic origin. Another clue is that the Rimae Prinz region has many known volcanic features such as sinuous rilles and pit craters. The lack of a raised rim, and the surrounding volcanic features, is certainly consistent with a volcano-tectonic collapse origin, later partially flooded with mare basalt from a nearby vent. Or perhaps this crater was a vent itself, and its final eruptions nearly filled it up. A full understanding of how this feature formed may require an on-site investigation.
Explore the full NAC below, perhaps other clues to the origin of this buried crater can be located nearby.
Related Posts:
Brayley G
Rimae Prinz Region - Constellation Region of Interest
Lunar Kipuka
Rilles as far as the eye can see in Prinz!
Published by Raquel Nuno on 15 August 2013